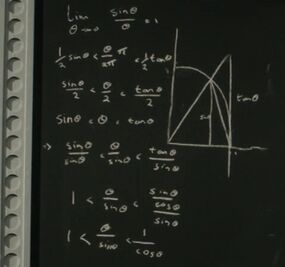1 (number): Difference between revisions
m (Bot: Cosmetic changes) |
No edit summary |
||
| Line 7: | Line 7: | ||
[[File:Calculus demonstration 1.jpg|thumb|Part of the [[Mathematical proof|demonstration]] made by the [[Twelfth Doctor]]. ([[TV]]: ''[[The Pilot (TV story)|The Pilot]]'')]] | [[File:Calculus demonstration 1.jpg|thumb|Part of the [[Mathematical proof|demonstration]] made by the [[Twelfth Doctor]]. ([[TV]]: ''[[The Pilot (TV story)|The Pilot]]'')]] | ||
The [[Twelfth Doctor]] once [[Mathematics|proved]] that <math>\lim_{\theta\to 0} \frac {sin \theta} {\theta} = 1</math>. ([[TV]]: ''[[The Pilot (TV story)|The Pilot]]'') | The [[Twelfth Doctor]] once [[Mathematics|proved]] that <math>\lim_{\theta\to 0} \frac {sin \theta} {\theta} = 1</math>. ([[TV]]: ''[[The Pilot (TV story)|The Pilot]]'') | ||
[[Block Transfer Computation]] made use of 1s and [[0 (number)|0]]s, as it was written in [[binary]]. ([[AUDIO]]: ''[[The Enchantress of Numbers (audio story)|The Enchantress of Numbers]]'') | |||
According to the [[Second Doctor]], a one in [[13 (number)|13]] chance was about [[7.6923 (number)|7.6923]] [[percentage|percent]], [[odds]] he didn't like. ([[COMIC]]: ''[[Card Conundrum (comic story)|Card Conundrum]]'') | According to the [[Second Doctor]], a one in [[13 (number)|13]] chance was about [[7.6923 (number)|7.6923]] [[percentage|percent]], [[odds]] he didn't like. ([[COMIC]]: ''[[Card Conundrum (comic story)|Card Conundrum]]'') | ||
| Line 21: | Line 23: | ||
== Footnotes == | == Footnotes == | ||
{{reflist}} | {{reflist}} | ||
[[Category:Prime numbers|N 0001]] | [[Category:Prime numbers|N 0001]] | ||
Revision as of 07:00, 1 November 2019
1 was a prime number. (AUDIO: The Haunting)
According to the Tenth Doctor, "Any number that reduces to 1 when you take the sum of the square of its digits and continue iterating it until it yields 1 is a happy number; any number that doesn't, isn't." (TV: 42)
The Twelfth Doctor once proved that . (TV: The Pilot)
Block Transfer Computation made use of 1s and 0s, as it was written in binary. (AUDIO: The Enchantress of Numbers)
According to the Second Doctor, a one in 13 chance was about 7.6923 percent, odds he didn't like. (COMIC: Card Conundrum)
The Twelfth Doctor once told Bill that "eleven plus two" was an anagram of "twelve plus one", to which Bill responded that both of these were equal to 13. (COMIC: Harvest of the Daleks)
Behind the scenes
Though AUDIO: The Haunting establishes that 1 is itself a prime number in the DWU, this is a point of contention among mathematicians.
Generally, 1 is considered neither prime nor composite. It would certainly have been considered a prime, however, in the story's time period of the 1890s. In particular, the entry for Number published in 1890 in the 9th edition of Encyclopædia Britannica stated that every positive number was either prime or composite, and explicitly listed 1 as prime.[1]
Though unremarked in PROSE: Daisy Chain, 1 is also the first and second Fibonacci number.
Footnotes
- ↑ A. Reddick et al. The History of the Primality of One---A Selection of Sources. Accessed at http://primes.utm.edu/notes/one.pdf on 7.12.2015.